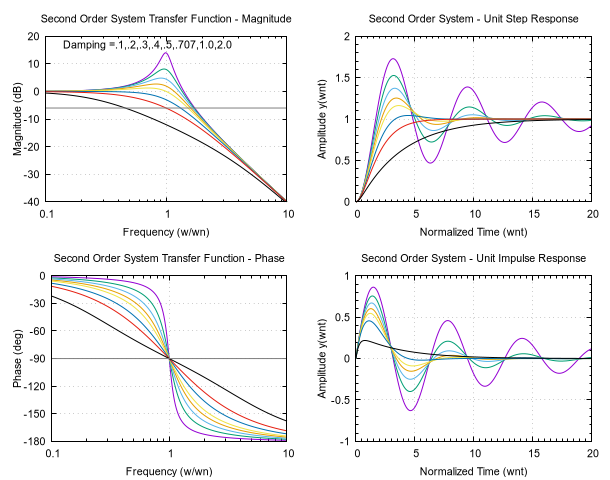
# GNUPLOT v3.6 beta multiplot script file # # Second Order System Characteristics # # D**2 + 2*zeta*wn*D + (wn**2)y = (wn**2)*x # # x input variable # y output variable # w frequency ratio (w/wn) # wn natural frequency # wd damped natural frequency # zeta damping ratio # mag(w) amplitude response # phi(w) phase response # wdwn damped natural frequency ratio # wnt normalized time # # Plots: # Frequency domain magnitude response # phase response # # Time domain unit step response # unit impulse response # # # Created by: W. D. Kirby email: wdkirby@ix.netcom.com # Date: 1/18/96 # Released to the public domain with no warranty of any kind # set style function lines set size 1.0, 1.0 set origin 0.0, 0.0 set multiplot set size 0.5,0.5 set origin 0.0,0.5 set grid unset key set angles radians set samples 250 # EAM Dec 2024 - reset to defaults so that "remultiplot" reproduces the original set xtics auto set mxtics default set ytics auto set mytics default # # Plot Magnitude Response set title "Second Order System Transfer Function - Magnitude" mag(w) = -10*log10( (1-w**2)**2 + 4*(zeta*w)**2) set dummy w set logscale x set xlabel "Frequency (w/wn)" set ylabel "Magnitude (dB)" offset 1,0 set label 1 "Damping =.1,.2,.3,.4,.5,.707,1.0,2.0" at .14,17 set xrange [.1:10] set yrange [-40:20] plot \ zeta=.1,mag(w), \ zeta=.2,mag(w), \ zeta=.3,mag(w), \ zeta=.4,mag(w), \ zeta=.5,mag(w), \ zeta=.707,mag(w), \ zeta=1.0,mag(w), \ zeta=2.0,mag(w),-6 # # Plot Phase Response set size 0.5,0.5 set origin 0.0,0.0 set title "Second Order System Transfer Function - Phase" set label 1 "" set ylabel "Phase (deg)" offset 1,0 set ytics -180, 30, 0 set yrange [-180:0] tmp(w) = (-180/pi)*atan( 2*zeta*w/(1-w**2) ) # Fix for atan function wrap problem tmp1(w)= w<1?tmp(w):(tmp(w)-180) phi(w)=zeta==1?(-2*(180/pi)*atan(w)):tmp1(w) plot \ zeta=.1,phi(w), \ zeta=.2,phi(w), \ zeta=.3,phi(w), \ zeta=.4,phi(w), \ zeta=.5,phi(w), \ zeta=.707,phi(w), \ zeta=1,phi(w), \ zeta=2.0,phi(w), \ -90 # # Plot Step Response set size 0.5,0.5 set origin 0.5,0.5 set dummy wnt unset logscale x set title "Second Order System - Unit Step Response" set ylabel "Amplitude y(wnt)" offset 1,0 set xlabel "Normalized Time (wnt)" set xrange [0:20] set xtics 0,5,20 set yrange [0:2.0] set ytics 0, .5, 2.0 set mytics 5 set mxtics 10 wdwn(zeta)=sqrt(1-zeta**2) shift(zeta) = atan(wdwn(zeta)/zeta) alpha(zeta)=zeta>1?sqrt(zeta**2-1.0):0 tau1(zeta)=1/(zeta-alpha(zeta)) tau2(zeta)=1/(zeta+alpha(zeta)) c1(zeta)=(zeta + alpha(zeta))/(2*alpha(zeta)) c2(zeta)=c1(zeta)-1 y1(wnt)=zeta==1?1 - exp(-wnt)*(wnt + 1):0 y2(wnt)=zeta<1?(1 - (exp(-zeta*wnt)/wdwn(zeta))*sin(wdwn(zeta)*wnt + shift(zeta))):y1(wnt) y(wnt)=zeta>1?1-c1(zeta)*exp(-wnt/tau1(zeta))+c2(zeta)*exp(-wnt/tau2(zeta)):y2(wnt) plot \ zeta=.1,y(wnt), \ zeta=.2,y(wnt), \ zeta=.3,y(wnt), \ zeta=.4,y(wnt), \ zeta=.5,y(wnt), \ zeta=.707,y(wnt), \ zeta=1,y(wnt), \ zeta=2,y(wnt) # # Plot Impulse Response set origin .5,0. set title "Second Order System - Unit Impulse Response" y(wnt)=exp(-zeta*wnt) * sin(wdwn(zeta)*wnt) / wdwn(zeta) set yrange [-1. :1.] set ytics -1,.5,1. plot \ zeta=.1,y(wnt), \ zeta=.2,y(wnt), \ zeta=.3,y(wnt), \ zeta=.4,y(wnt), \ zeta=.5,y(wnt), \ zeta=.707,y(wnt), \ zeta=1,y(wnt), \ zeta=2,y(wnt) unset multiplotClick here for minimal script to generate this plot
