# Demo Statistical Approximations version 1.1
#
# Copyright (c) 1991, Jos van der Woude, jvdwoude@hut.nl
# History:
# -- --- 1991 Jos van der Woude: 1st version
# 06 Jun 2006 Dan Sebald: Added plot methods for better visual effect.
print " Statistical Approximations, version 1.1"
print ""
print " Copyright (c) 1991, 1992, Jos van de Woude, jvdwoude@hut.nl"
print ""
save_encoding = GPVAL_ENCODING
set encoding utf8
load "stat.inc"
rnd(x) = floor(x+0.5)
r_xmin = -1
r_sigma = 4.0
# Binomial PDF using normal approximation
n = 25; p = 0.15
mu = n * p
sigma = sqrt(n * p * (1.0 - p))
xmin = floor(mu - r_sigma * sigma)
xmin = xmin < r_xmin ? r_xmin : xmin
xmax = ceil(mu + r_sigma * sigma)
ymax = 1.1 * binom(floor((n+1)*p), n, p) #mode of binomial PDF used
set key box
unset zeroaxis
set xrange [xmin - 1 : xmax + 1]
set yrange [0 : ymax]
set xlabel "k, x"
set ylabel "probability density"
set ytics 0, ymax / 10.0, ymax
set format x "%2.0f"
set format y "%3.2f"
set sample 200
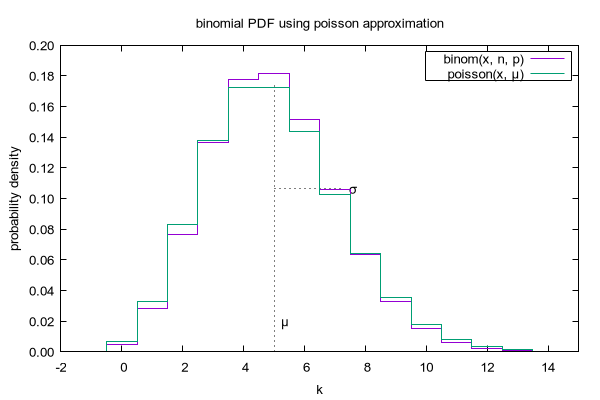
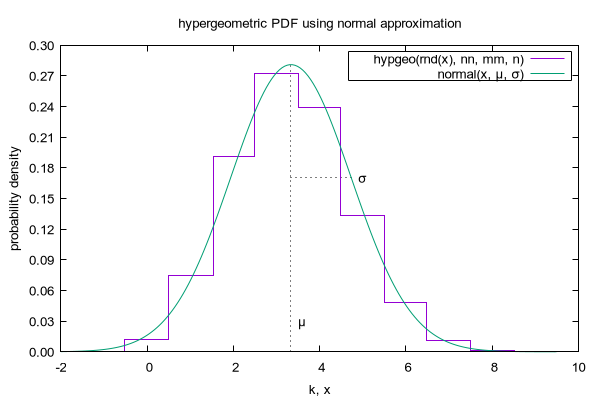
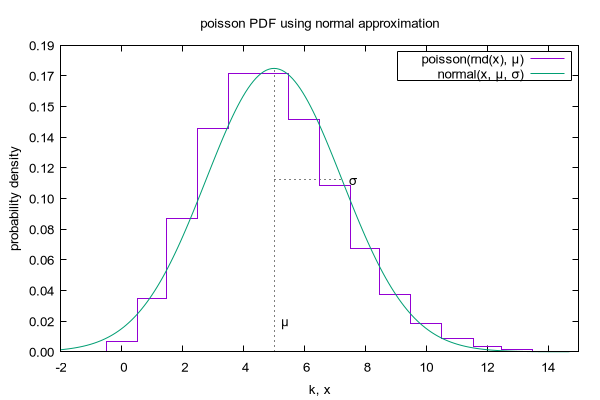
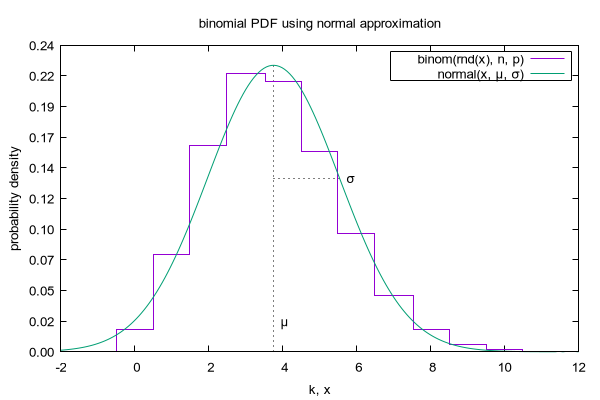
set title "binomial PDF using normal approximation"
set arrow from mu, 0 to mu, normal(mu, mu, sigma) nohead dt 3
set arrow from mu, normal(mu + sigma, mu, sigma) \
to mu + sigma, normal(mu + sigma, mu, sigma) nohead dt 3
set label "μ" at mu, ymax / 10 offset 1, 0
set label "σ" at mu + sigma, normal(mu + sigma, mu, sigma) offset 1, 0
plot binom(rnd(x), n, p) with histeps, normal(x, mu, sigma) t "normal(x, μ, σ)"
Click here for minimal script to generate this plot